Willkommen zum 2. Part meines ziemlich komplexen Blog. Jetzt wirds praktisch. Und damit auch zum für mich schwersten Teil. Das Problem liegt darin das wir es nun mit der realen Welt zu tun haben, also mit Motoren, Zeit und Raum. Hier herrscht demnach die größte Fehleranfälligkeit, wenn Motoren nicht so fahren wie sie eigentlich sollen da minimale Abweichungen von den Berechnungen große Änderungen am Graphen auslösen können. Naja fangen wir mal an.
Grundlegend ist die Korrelation zwischen der Winkelgeschwindigkeit und Bahngeschwindigkeit/Geschwindigkeit. Die Winkelgeschwindigkeit ist dabei der Winkel der in einem Zeitintervall zurückgelegt wird und die Bahngeschwindigkeit die zurückgelegte Strecke auf der Kreisbahn (die gleichgroß wie die auf der Geraden ist). Die Motoren arbeiten mit Winkelgeschwindigkeiten, die letztendlich auf eine Gerade übertragen werden. Dafür berechnen wir einen „Angle Ratio„, der sich aus dem durchschnittlichen Durchmesser eines Zahnrads * π * 1/360 ergibt. Kurze Erläuterung: Durchmesser * π = Umfang des Kreises, mal 1/360 entspricht sozusagen 1° der Kreisbahn. Multiplizieren wir nun eine Winkelgeschwindigkeit mit dem gerade ausgerechneten Angle Ratio erhalten wir eine Distanz, Dividieren wir Distanz und Angle Ratio erhalten wir einen Winkel. Da das für den weiteren Verlauf eigentlich nur Schreibaufwand ist, müsst ihr euch merken das Motoren mit Winkeln arbeiten, Positionen aber natürlich in Distanzen angegeben sind.
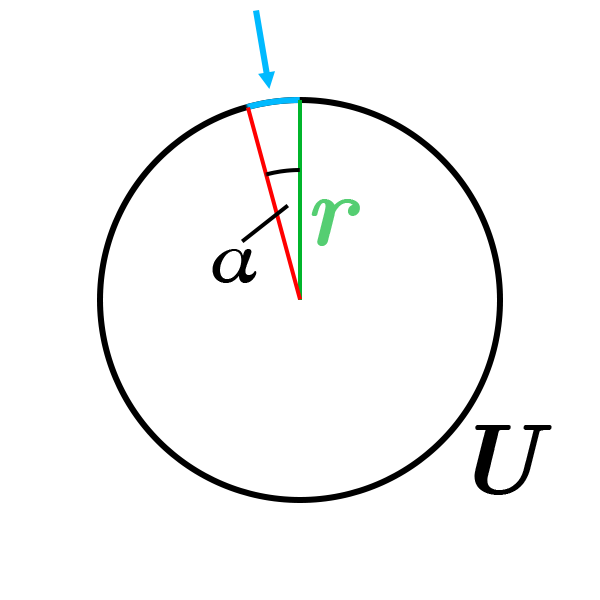
Für die Übersetzung der Zahnradketten muss ich mir zum Glück keine Gedanken machen, dass macht die Software automatisch, man muss nur die Zähne abzählen und eingeben. 😃
Erster Versuch
Unser erster Versuch bestand darin den x-Motor für eine bestimmte Zeit laufen zu lassen und dann einfach mal die y-Geschwindigkeit auf gut Glück sehr oft anpassen. Zwar war das nur eine temporäre Lösung, dennnoch war dieser Test sehr wichtig um zu checken, ob verwertbare Ergebnisse dabei rauskommen. Und tatsächlich, man hat erkannt wie der Stift Kurven gezeichnet hat und auch nur ein wenig gestockt hat.
Deshalb habe ich begonnen die Strategie auszufeilen bis ein ähnliches Konzept rauskam:
Verbesserung
Die Strategie basiert wieder darauf, den x-Motor mit einer konstanten Geschwindigkeit fahren lassen und in bestimmten Zeitintervallen die Geschwindigkeit des y-Motor anzupassen. Die Geschwindigkeit lässt sich dabei als die momentane Änderungsrate oder auch als Ableitung an der Stelle x deuten. Wer sich jetzt denkt: Ableitung? Was, wie, wo, warum?“, empfehle ich das Video von simpleclub.
Die genauen Schritte sehen dabei so aus:
- Gehe zum sichtbaren Anfang der Funktion
- Berechne anhand der Anzahl der Zeitintervalle wie lang ein Intervall ist
- Solange die aktuelle Position des Stiftes noch nicht am Ende ist:
- Berechne die Geschwindigkeit des y-Motors
- Falls diese die physikalische Grenzgeschwindigkeit des Motors überschreitet, verlangsame den x-Motor so stark, dass das Verhältnis von x zu y noch stimmt
- Berechne, wie lange das Zeitintervall in der Realität ist (wenn der x-Motor verlangsamt wurde, muss ein Zeitintervall länger sein damit der x-Motor pro Intervall die gleiche Distanz zurücklegt)
- Starte die Motoren!
Erläuterung
1: Um den sichtbaren Start zu finden fangen wir einfach links an und gucken ob der y-Wert in unserem gültigen Bereich liegt. Wenn nicht, guckt man einfach ein bisschen weiter rechts. Bis man am Ende ist.
2: Das Intervall entspricht der Gesamtzeit durch die Präzision (Anzahl der Intervalle), die Gesamtzeit habe ich mithilfe der Länge der x-Achse und der Geschwindigkeit des x-Motors berechnet.
3: Hier ist meiner Meinung nach das größte Fehlerpotential. Aktuell rechne ich zusätzlich aus, wie viel mm der x-Motor hypothetisch pro Intervall zurücklegen sollte (x-Speed * Zeit, s = v * t → Ist das Physik? 🦋). Rein rechnerisch sollte das auch stimmen.
Draw Loop
1: Wie vorher die Ableitung an der aktuellen Stelle x.
2: Hier wird ein „Speed Factor“ ausgerechnet: Das Verhältnis von der y-Geschwindigkeit zur maximalen y-Geschwindigkeit. Um das Verhältnis von x zu y einzuhalten, wird die Geschwindigkeit durch diesen Faktor geteilt
3: Zeit sollte die durchschnittliche Zeit multipliziert mit dem Speed Factor sein
Ergebnis
Der Graph wird nicht korrekt abgebildet. Meistens ist er etwas zu breit geraten und generell auch zu hoch. Ich saß insgesamt ziemlich lange daran Fehlerquellen zu suchen, keine Lösung ließ war für das Originalproblem verantwortlich. Irgendwann begann ich auch zufällige Konstanten einzubauen die dann für ein paar bessere Graphen sorgten, bei anderen Funktionen den Motor jedoch bis zum Anschlag fahren lassen haben, was natürlich nicht korrekt ist.
 <
<