Was ist Minimax? Minimax ist ein Algorithmus, mit dem man, z.B. bei einem Zweispielerspiel wie Tic-Tac-Toe den besten Zug, den man machen kann, rausfinden kann, indem man alle Spielzüge simuliert, und anhand der Ergebnisse schaut welcher Zug das beste Ergebnis liefert. Dies passiert, indem es einen minimierenden und einen maximierenden Spieler gibt, der minimierende probiert das kleinste Ergebnis zu bekommen und der maximierende das Größte. Wenn nach einer kompletten Simulation der Züge also rauskommt, dass der minimierende Spieler gewinnt, ist das Ergebnis z.B. -1, bei einem Unentschieden z.B. 0 und wenn der maximierende Spieler gewinnt, z.B. 1. Anhand aller Ergebnisse sucht sich dann der Spieler, der an der Reihe ist, ein Zug aus, der für ihn am besten ist.
Kleines Beispiel:
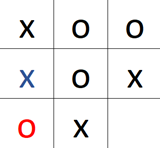
 Das ist ein Spielfeld mitten aus einem Spiel. Nun ist x am Zug. X ist hierbei der maximierende Spieler.
Das ist ein Spielfeld mitten aus einem Spiel. Nun ist x am Zug. X ist hierbei der maximierende Spieler.
Daraus folgen dann folgende Züge:
1) 2) 3)
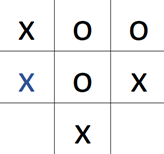
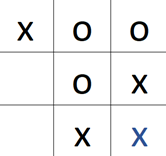
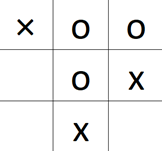
Da das spiel noch nicht zu Ende ist, wird dies nun weitergespielt.
Für die erste Möglichkeit, den Zug zu machen, gäbe es dann folgende nachfolgende Züge:
1.1) 1.2)

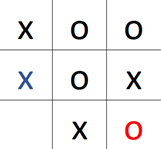
Score: -1, da o gewinnt!
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀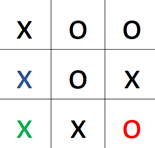
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Score +1 da x gewinnt!
1.1 bekommt den Wert -1, da o gewinnt. Bei 1.2 bekommt das Feld dann den Wert +1, da in dem Nachfolgenden Zug das Spiel beendet wird und x gewinnt. Nun muss sich der Spieler o für einen dieser Züge entscheiden. Da o der minimierende Spieler ist entscheidet dieser sich für den kleinsten Wert dieser beiden. Das bedeutet -1 also für 1.1. Eine Etage darüber würde x sich dann nach allen simulierten Möglichkeiten für den höchsten der gegebenen Werte entscheiden, wenn man sich alle möglichen Züge angeguckt hat.
In Python kann ich dann eine Funktion schreiben die genau das überprüft. Dies passiert am einfachsten mit einer Rekursiven Funktion. Eine Rekursive Funktion ist eine Funktion, die sich innerhalb bis zu einem bestimmten Punkt immer wieder selbst aufruft, bis sie dann irgendwann auf ein Ergebnis kommt und dieses dann bis nach ganz oben transportiert.
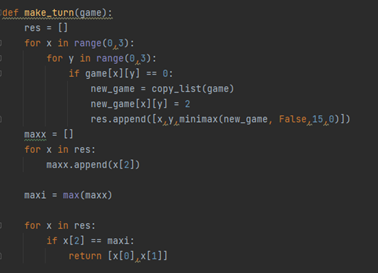
In meinem Code benutze ich dafür dann zwei Funktionen. make_turn() sucht für mich jede Möglichkeit raus, wie der Roboter seinen Zug machen kann, mit diesen Möglichkeiten ruft er dann den Minimax Algorithmus auf. Dafür braucht dieser die Informationen des Feldes, die Info welcher Spieler als nächstes dran ist, die Anzahl der Züge, die er maximal in die Tiefe gehen soll, die er zwar nicht dringend braucht, weil er in diesem Fall alle Züge ausprobieren soll aber aus Testzwecken habe ich das trotzdem eingebaut und als letztes noch die Tiefe in der er gerade ist. Ich mache das alles in zwei verschiedenen Funktionen, da ich mit der ersten Funktion auseinanderhalten kann welcher Zug welches Ergebnis zur Folge hat und ich mich somit für den besten Zug entscheiden kann. Bei der Funktion minimax() ist es egal, welcher Zug welches Ergebnis zu Folge hat, da das noch in der Zukunft ist und deswegen der Roboter nur beim nächsten Zug wissen muss auf welches Feld dieser verweist. Sobald alle Ergebnisse da sind, checkt diese Funktion nur noch welcher Zug das höchste Ergebnis zur Folge hat, da der Computer der maximierende Spieler ist.
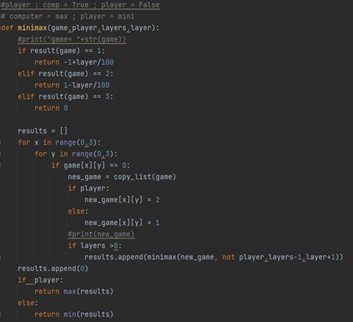
Die minimax() Funktion führ dann den Minimax Algorithmus bis zum Ende durch, so wie oben erklärt. Als kleinen Zusatz habe ich noch eine Möglichkeit mir überlegt, wie der Roboter unnötige Züge überspringen kann, da der Roboter nach dem Prinzip wie es oben beschrieben ist zu Anfang noch jedes mögliche Feld in Betracht zieht, da er selbst bei der ersten Reihe |x| |o| auch noch ein Kreuz in der Mitte setzen würde, da er das Spiel am Ende trotzdem noch gewinnen könnte. Aus diesem Grund habe ich den Parameter „layer“ eingefügt. Mit diesem Parameter kann ich bestimmen in welcher Lage man ist. Mit dieser Information ändere ich dann das Ergebnis dann leicht ab, so dass das Ergebnis des maximierenden Spielers z.B. um die Tiefe/100 nach unten verändert wird. Dadurch nimmt der Roboter Möglichkeiten wo er gewinnen kann die nicht so tief liegen lieber als Ergebnisse, wo er z.B. erst in der letzten Runde gewinnen kann. Aus diesem Grund werden dann unnötige Züge übersprungen.
Wenn der Algorithmus so tief angekommen ist, dass das Spiel vorbei ist, wird dieser Wert dann am Anfang der Funktion an die vorherigen Durchgänge übergeben(siehe Bild). Falls dies nicht der Fall ist wird darunter geguckt an welchen Stellen noch niemand etwas gesetzt hat, dann wird für jede dieser Möglichkeiten ein neues Feld erzeugt, die entsprechende Figur eingesetzt und die minimax Funktion erneut aufgerufen, dies geschieht mit dem neuen Spielfeld, dem jeweils anderen Spieler-boolean, „layers-1“ wichtig falls ich nur eine bestimmte Anzahl an Zügen in die Tiefe gehen will und dann die aktuelle Tiefe +1 namens „layer“. Sobald die Funktion dann alle Werte unter sich bekommen hat, sucht sie den jeweils besten raus und gibt diesen dann weiter nach oben.
Am Ende sucht sich die Funktion make_turn() den höchsten Wert von allen Zügen aus und macht dann den besten Zug.
